Homework 2
Due at 11:59:59 pm on 2/12/2021.
Instructions
Download hw02.zip. Inside the archive, you will find starter files for the questions in this homework, along with a copy of the OK autograder.
Submission: When you are done, submit with python3 ok --submit. You may submit more than once before the deadline; only the final submission will be scored. Check that you have successfully submitted your code on okpy.org. See this article for more instructions on okpy and submitting assignments.
Readings: This homework relies on following references:
To submit: run ok with the --submit option:
python3 ok --submitQuestions
Question 1: Fibonacci
The Fibonacci sequence is a famous sequence in mathematics. The first element in the sequence is 0 and the second element is 1. The nth element is defined as Fn = Fn-1 + Fn-2.
Implement the fib function, which takes an integer n and returns
the nth Fibonacci number. Use a while loop in your solution.
def fib(n):
"""Returns the nth Fibonacci number.
>>> fib(0)
0
>>> fib(1)
1
>>> fib(2)
1
>>> fib(3)
2
>>> fib(4)
3
>>> fib(5)
5
>>> fib(6)
8
>>> fib(100)
354224848179261915075
"""
"*** YOUR CODE HERE ***"Use OK to test your code:
python3 ok -q fibQuestion 2: Mul_by_num
Using higher order functions, complete the mul_by_num function. This
function should take an argument and return a one argument function
that multiplies any value passed to it by the original number.
def mul_by_num(factor):
"""
Returns a function that takes one argument and returns num
times that argument.
>>> x = mul_by_num(5)
>>> y = mul_by_num(2)
>>> x(3)
15
>>> y(-4)
-8
"""
"*** YOUR CODE HERE ***"
Use OK to test your code:
python3 ok -q mul_by_numQuestion 3: This Question is so Derivative
Define a function make_derivative that returns a function: the derivative of a
function f. Assuming that f is a single-variable mathematical function, its
derivative will also be a single-variable function. When called with a number
a, the derivative will estimate the slope of f at point (a, f(a)).
Recall that the formula for finding the derivative of f at point a is:
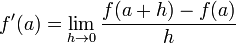
where h approaches 0. We will approximate the derivative by choosing a very
small value for h. The closer h is to 0, the better the estimate of the
derivative will be.
def make_derivative(f):
"""Returns a function that approximates the derivative of f.
Recall that f'(a) = (f(a + h) - f(a)) / h as h approaches 0. We will
approximate the derivative by choosing a very small value for h.
>>> def square(x):
... # equivalent to: square = lambda x: x*x
... return x*x
>>> derivative = make_derivative(square)
>>> result = derivative(3)
>>> round(result, 3) # approximately 2*3
6.0
"""
h=0.00001
"*** YOUR CODE HERE ***"Use OK to test your code:
python3 ok -q make_derivativeQuestion 4: Count van Count
Consider the following implementations of count_factors and count_primes:
def count_factors(n):
"""Return the number of positive factors that n has."""
i, count = 1, 0
while i <= n:
if n % i == 0:
count += 1
i += 1
return count
def count_primes(n):
"""Return the number of prime numbers up to and including n."""
i, count = 1, 0
while i <= n:
if is_prime(i):
count += 1
i += 1
return count
def is_prime(n):
return count_factors(n) == 2 # only factors are 1 and nThe implementations look quite similar! Generalize this logic by writing a
function count_cond, which takes in a two-argument predicate function mystery_function(n,
i). count_cond returns a count of all the numbers from 1 to n that satisfy
condition.
Note: A predicate function is a function that returns a boolean (True or False).
def count_cond(mystery_function, n):
"""
>>> def divisible(n, i):
... return n % i == 0
>>> count_cond(divisible, 2) # 1, 2
2
>>> count_cond(divisible, 4) # 1, 2, 4
3
>>> count_cond(divisible, 12) # 1, 2, 3, 4, 6, 12
6
>>> def is_prime(n, i):
... return count_cond(divisible, i) == 2
>>> count_cond(is_prime, 2) # 2
1
>>> count_cond(is_prime, 3) # 2, 3
2
>>> count_cond(is_prime, 4) # 2, 3
2
>>> count_cond(is_prime, 5) # 2, 3, 5
3
>>> count_cond(is_prime, 20) # 2, 3, 5, 7, 11, 13, 17, 19
8
"""
"*** YOUR CODE HERE ***"
Use OK to test your code:
python3 ok -q count_condQuestion 5: I Heard You Liked Functions...
Define a function cycle that takes in three functions f1, f2,
f3, as arguments. cycle will return another function that should
take in an integer argument n and return another function. That
final function should take in an argument x and cycle through
applying f1, f2, and f3 to x, depending on what n
was. Here's the what the final function should do to x for a few
values of n:
n = 0, returnxn = 1, applyf1tox, or returnf1(x)n = 2, applyf1toxand thenf2to the result of that, or returnf2(f1(x))n = 3, applyf1tox,f2to the result of applyingf1, and thenf3to the result of applyingf2, orf3(f2(f1(x)))n = 4, start the cycle again applyingf1, thenf2, thenf3, thenf1again, orf1(f3(f2(f1(x))))- And so forth.
Hint: most of the work goes inside the most nested function.
def cycle(f1, f2, f3):
""" Returns a function that is itself a higher order function
>>> def add1(x):
... return x + 1
>>> def times2(x):
... return x * 2
>>> def add3(x):
... return x + 3
>>> my_cycle = cycle(add1, times2, add3)
>>> identity = my_cycle(0)
>>> identity(5)
5
>>> add_one_then_double = my_cycle(2)
>>> add_one_then_double(1)
4
>>> do_all_functions = my_cycle(3)
>>> do_all_functions(2)
9
>>> do_more_than_a_cycle = my_cycle(4)
>>> do_more_than_a_cycle(2)
10
>>> do_two_cycles = my_cycle(6)
>>> do_two_cycles(1)
19
"""
"*** YOUR CODE HERE ***"Use OK to test your code:
python3 ok -q cycleSubmit
Make sure to submit this assignment by running:
python3 ok --submit