Due at 11:59:59 pm on Friday, 2/21/2020.

Starter Files

Download lab03.zip. Inside the archive, you will find starter files for the questions in this lab, along with a copy of the OK autograder.

Submission

By the end of this lab, you should have submitted the lab with python3 ok --submit. You may submit more than once before the deadline; only the final submission will be graded. Check that you have successfully submitted your code on okpy.org. See this article for more instructions on okpy and submitting assignments.

• To receive full credit for this lab, all questions 1 - 4 must be attempted. Question 5 is an optional question.

When you are ready to submit, run ok with the --submit option:

python3 ok --submit

After submitting, ok will display a submission URL, with which you can view your submission on okpy.org.

Python Tutor

Python tutor is a website that allows you to write python code in your web browser and see it visualized step by step. Before we explain more, let’s experiment with it a little. First, head to the python tutor website

Copy and paste this code snippet into the box:

y = 3
x = 5
z = y + x
print(z)

Press “visualize execution”

You can press the “forward” and “back” buttons to step forward or backwards in the code. Every time you step forward, python will run that line of code. Notice the legend on the bottom left of the visualizer that tells you what the color of the arrows mean.

You may notice that when you press the forward button for the first time, something pops up on the right side of the screen.

Given the line that you just ran, what do you think this diagram means? Try running a few more lines.

What python tutor is doing is showing you exactly what each variable is and what its value is., It shows you the output of the print statement in the box above the diagram.

What’s the difference between the value that appears in the interpreter after evaluating an expression and the output displayed by a print statement?

The value that appears after evaluating is a feature that only the interpreter has. When you actually run the code from a file, that return value does not get printed. The print statement actually does print directly to your terminal.

Python tutor is a great tool because it helps you understand exactly what your code is doing and also keeps track of what variables’ values are along the way. If you ever have trouble understanding what your code is doing, or finding a bug, pull up python tutor and step through it!

When we assign variables, python tutor visualizes this with the variable’s name and a box next to it with the variable’s value. This is just what a variable is! Something that can get assigned a value.

The frame is called “global” for a reason. We will explain that later on.

Let’s throw a function in there. Copy and paste this into the python tutor:

from operator import add
y = 3
x = 5
z = add(x,y)
print(z)

If you step until step 5, we see that there is something under the “objects” category.

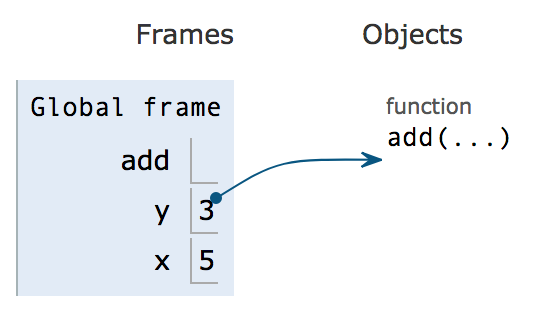
Add is a function, and functions live in object land. We denote which names correspond to which functions with an arrow.

You can think of everything in “frame land” as a box. The box holds something, but is not the thing itself. Some boxes hold integers directly, like the values of x and y in the above image. Other boxes hold more complicated things like functions which cannot be stored directly in the box. Instead, the box holds a pointer to the function which actually lives in object land. In this lab, we are not worried about that, we want you to pay attention to the boxes.

What about floats, booleans, and strings? They also live inside the box, as seen below.

Now that you understand a little bit of how python tutor works, let’s write a function to visualize.

Functions and Python Tutor

Let’s see what function calls look like in the python interpreter.

Paste this code into the interpreter. If you are not in edit mode, click the “edit this code” hyperlink.

def sum(x,y):
	z = x + y
	return z
x = 3
y = 4
z = sum(x,y)
a = z + 1

Now step through the code. Notice in step 5 something interesting happens. A new frame pops up and the execution arrow miraculously moves all the way to the first line. How did we get back there? Think about what would cause this jump before reading the answer below.

When we call the sum function, we need to step through the function itself and execute all of its lines. Where is the function defined? In line 1! Thus, the python interpreter needs to go back there and step through each individual line.

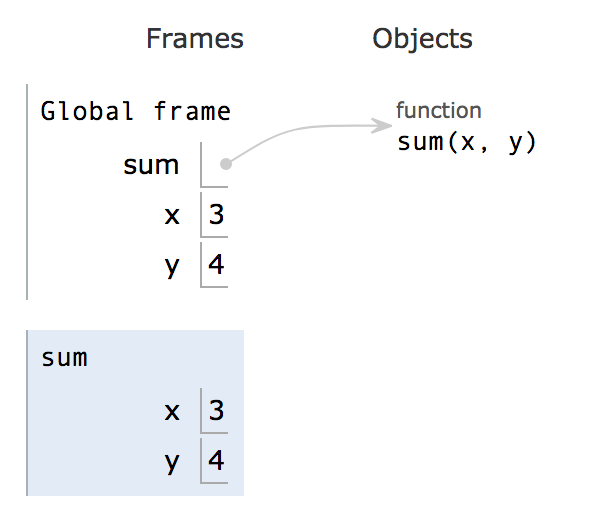
This new frame seen above is a local frame. It is a frame for the sum function that was just called. Everything that happens inside the sum function will be shown inside sum’s local frame.

Step through the rest of the code to see what happens.

Notice that between steps 8 and 9, the function jumps from line 3 to line 6. What’s that all about? Why doesn’t it just go straight to line 4?

Remember how the interpreter had to jump into the sum function to execute it? Well, when it finishes the function, it needs to jump back to the line it was running before the function. That line was line 6.

Now, let’s see what happens if a function calls a function. Copy the following code into python tutor.

def sum(x,y):
	z = x + y
	return z
def square_sum(x,y):
	z = 2
	return sum(x, y)**z
x = 3
y = 4
square_sum(x,y)

Now press “forward” 2 times.

You may notice that during steps 1 and 2, the visualizer skips over the bodies of the functions. This is because the functions have not been called yet, so the python interpreter will not unpack the function and go into it. It only notes that there are two functions named sum and square_sum, and assigns them to functions living in object land.

Try clicking forward to step 6. In step 6, the interpreter enters the square_sum function. See the new local frame that appeared.

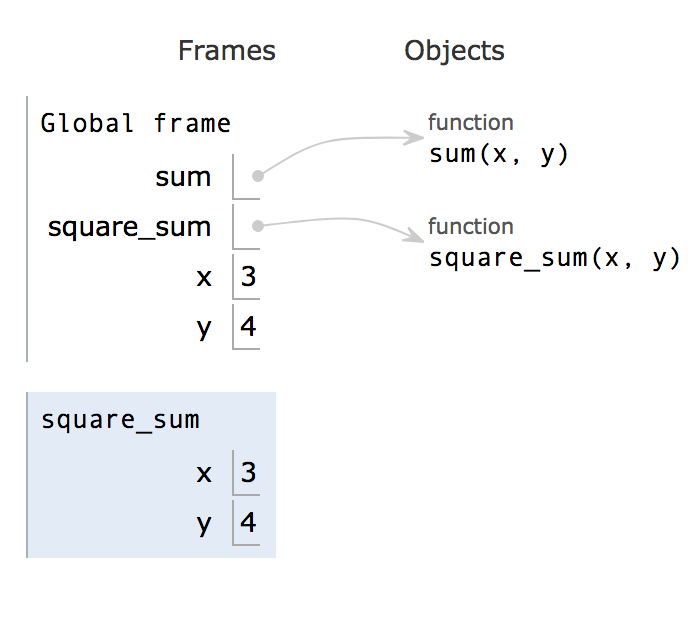
Fun fact: Because the frames are stacked this way, we call the group of frames the call stack.

If you click forward one more time, you’ll see z pop up, which is set to 2. Then, we enter the sum function. Step to step 11.

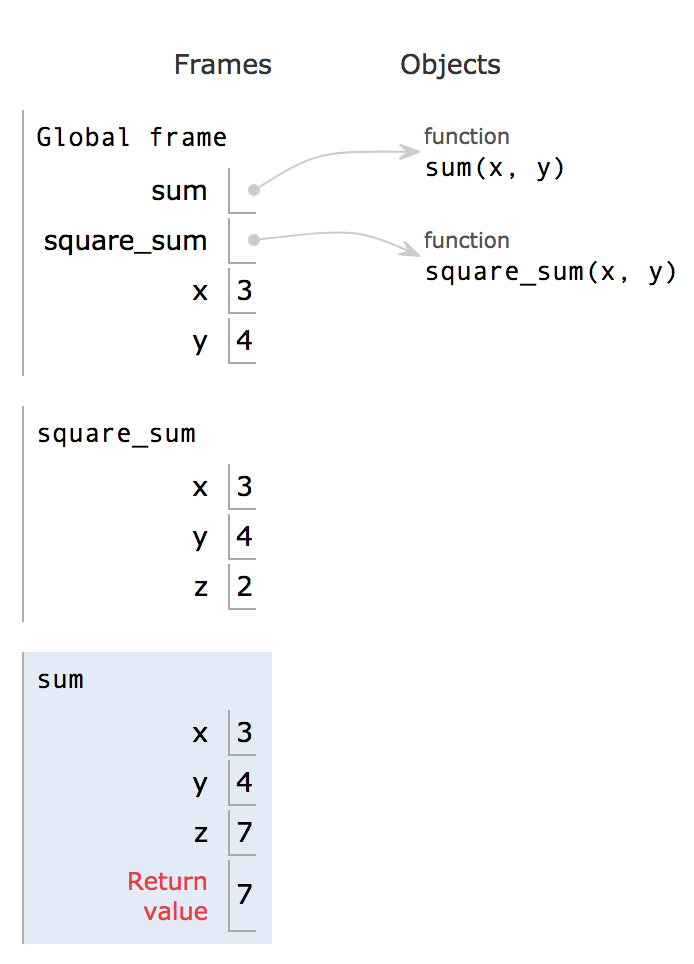
At this point, you see that we have many variables all names the same thing. How does python know which variable we are referring to when we want the value of “x”? Is it the first, the second, or the third?

This is where scope comes in.

Everything inside a function’s local frame is said to be in its “scope”. A functions scope contains all the variables and functions it can access/manipulate/use.

There are two big categories for scope: local and global.

• Global scope is just whatever lies in the global frame.
• Local scope is the scope of any individual function.

When we are in the sum function, when we ask for z, we will retrieve z in sum’s local frame. When we are in square_sum, we will retrieve the z in square_sum’s local frame.

Let’s continue exploring our function.

After returning from sum, we go back to the line where we called sum: 6. Now that we have the result of sum (7), we can raise it to the power of z, which is 2, and return it.

Now that you’ve seen a bit of defining functions, calling functions, and how both look like when they are visualized in python tutor, we will move on to learning about text editors.

Scopes and Nested Functions

Let’s see what nested function calls look like in the python interpreter.

PythonTutor

Paste this code into the interpreter or follow this link Ex1

def bonus(score):
    previousScore = score
    multiplier = 1
    if score > 25:
      multiplier = 2
    score *= multiplier
    return score
print(bonus(score))
print(previousScore)

Now step through the code. Why does it error out? The error message reads

NameError: name 'previousScore' is not defined

But didn't we define previousScore in the body of the bonus function? We did, but that previousScore is only defined in the scope of the function. So it is not accessible outside in the global scope.

Let's try another function Ex2

def totalScore(score):
    multiplier = 2
    def bonus(score):
      if score > 25:
        score *= multiplier
      else:
        score /= multiplier
      return score
  return score, bonus(score)
score = 12
totalScore(score)
print(score)

There's a lot to unpack here. We purposefully gave the variables the same names so you can see how python lookups values for variables. The general principle is that python looks for the value in the current scope first. If it can't find the variable there, it checks it's parent scope, and the parent's parent, all the way up to the global scope. If the variable still isn't found there, an error is raised. Walk through the lookup for multiplier on line 7 in your head as a sanity check.

List Comprehension

Question 1: Where Above

Lets use list comprehensions to implement some of the filters we could apply in Data 8's table.where() function. In particular, fill in the where_above function that returns a list that filters out any elements less than or equal to limit. Try to do this in only one line.

def where_above(lst, limit):
    """
    where_above behaves like table.where(column, are.above(limit)).
    The analogy is completed if you think of a column of a table as a list and return the filtered column instead of the entire table.

    >>> where_above([1, 2, 3], 2)
    [3]
    >>> where_above(range(13), 10)
    [11, 12]
    >>> where_above(range(123), 120)
    [121, 122]

    """
    "*** YOUR CODE HERE ***"
    
    return [n for n in lst if n > limit]

Toggle Solution

Use OK to test your code:

python3 ok -q where_above

Iteration

Question 2: Minmax

In c8 you often need to understand the spread of data. Write a simple function to find the minimum and maximum elements in a sequence using a for loop. You CANNOT use any in-built functions.

def minmax(s):
    """Return the minimum and maximum elements of a non-empty list. Hint: start 
    with defining two variables at the beginning. Do not use the built in 
    max or min functions

    >>> minmax([1, 2, -3])
    [-3, 2]
    >>> x = minmax([2])
    >>> x
    [2, 2]
    >>> minmax([4, 5, 4, 5, 1, 9, 0, 7])
    [0, 9]
    >>> minmax([100, -10, 1, 0, 10, -100])
    [-100, 100]
    """
    "*** YOUR CODE HERE ***"
    
    mn, mx = s[0], s[0]
    for x in s:
        if mn is None or x < mn:
            mn = x
        if mx is None or x > mx:
            mx = x
    return [mn, mx]

Toggle Solution

Use OK to test your code:

python3 ok -q minmax

Question 3: Common Member

Write a function common_member that takes in two lists lst1 and lst2 and returns True if they have at least one number in common. You can assume both the lists have at least one element.

def common_member(lst1, lst2):
    """
    Returns true if there are any common members between
    lst1 and lst2.
    >>> common_member([5, 3, 2, 1], [1, 9, 3, 4, 5])
    True
    >>> common_member([17, 18, 24], [23, 21, 22, 27, 29, 5])
    False
    >>> common_member([5, 7], [7, 3])
    True
    """
    "*** YOUR CODE HERE ***"
    for x in lst1:
        for y in lst2:
            if x == y:
                return True
    return False

Toggle Solution

Use OK to test your code:

python3 ok -q common_member

Question 4: Closest Power of 2

Let's test out our knowledge by making a function that finds the largest power of 2 that is less than a given number. Fill in the function closest_power_2 below to return the closest power of 2 using a while loop.

def closest_power_2(x):
    """ Returns the closest power of 2 that is less than x
    >>> closest_power_2(6)
    4
    >>> closest_power_2(32)
    16
    >>> closest_power_2(87)
    64
    >>> closest_power_2(4095)
    2048
    >>> closest_power_2(524290)
    524288
    """
    "*** YOUR CODE HERE ***"
    
    exponent = 0
    while x > (2 ** (exponent + 1)):
        exponent += 1
    return 2 ** exponent

Toggle Solution

Use OK to test your code:

python3 ok -q closest_power_2

Here's some food for thought: What mathematical operation is closely related to finding the closest power of 2? It's the logarithm! (at least with a base of 2) By keeping track of which power of 2 you are on, you can compute rounded down version of log base 2 of numbers using your closest_power_2 function. If this stuff is cool to you, you should check out CS61C, particularly the sections on binary representations of data, and bitwise operators.

Submit

Make sure to submit this assignment by running:

python3 ok --submit

---

Extra Credit Practice Open in a new window

These questions are new this semester. They're a mix of Parsons Problems, Code Tracing questions, and Code Writing questions.

Confused about how to use the tool? Check out https://codestyle.herokuapp.com/cs88-lab01 for some problems designed to demonstrate how to solve these types of problems.

These cover some similar material to lab, so can be helpful to further review or try to learn the material. Unlike lab and homework, after you've worked for long enough and tested your code enough times on any of these questions, you'll have the option to view an instructor solution. You'll unlock each question one at a time, either by correctly answering the previous question or by viewing an instructor solution.

Starting from lab 2 onward, each set of questions are worth half (0.5) a point per lab, for a total opportunity of 4-5 points throughout the semester.

Use OK to test your code:

python3 ok -q extra_credit

---

Optional Questions

Question 5: Total Price

Implement the function total_price, which takes in a list of prices of individual products and needs to find the total price. Unfortunately, any product that is priced greater than or equal to $20 has a 50 percent tax, so include that in the final price.

Try to do this in one line!

Cast your final answer to an integer to avoid floating point precision errors. For example, if x contains your final answer, return int(x)!

def total_price(prices):
    """
    Finds the total price of all products in prices including a
    50% tax on products with a price greater than or equal to 20.
    >>> total_price([5, 20, 30, 7])
    87
    >>> total_price([8, 4, 3])
    15
    >>> total_price([10, 100, 4])
    164
    """
    "*** YOUR CODE HERE ***"
    return int(sum([x if x < 20 else 1.5*x for x in prices]))

Toggle Solution

Use OK to test your code:

python3 ok -q total_price