Lab 7: More Recursion
Due at 11:59:59 pm on Tuesday, 10/19/2021.
Starter Files
Download lab07.zip. Inside the archive, you will find starter files for the questions in this lab, along with a copy of the OK autograder.
Submission
By the end of this lab, you should have submitted the lab with python3 ok --submit. You may submit more than once before the deadline; only the final submission will be graded. Check that you have successfully submitted your code on okpy.org. See this article for more instructions on okpy and submitting assignments.
- Submit the
lab07.pyfile took.
Questions
Question 1: Sum Digit Differences
Write the recursive function sum_diffs which takes in n, a number, and
returns the sum of the differences between adjacent digits in the number n.
def sum_diffs(n):
""" Return the sum of the differences between adjacent digits in the number n.
>>> sum_diffs(8)
0
>>> sum_diffs(154) # 4 + 1 = 5
5
>>> sum_diffs(12321) # 1 + 1 + 1 + 1
4
>>> sum_diffs(7351) # 4 + 2 + 4
10
"""
"*** YOUR CODE HERE ***"
if n < 10:
return 0
else:
dif = abs(n % 10 - (n // 10)% 10)
return dif + sum_diffs(n // 10)Use OK to test your code:
python3 ok -q sum_diffsQuestion 2: Insect Combinatorics
Consider an insect in an M by N grid. The insect starts at the
bottom left corner, (0, 0), and wants to end up at the top right
corner, (M-1, N-1). The insect is only capable of moving right or
up. Write a function paths that takes a grid length and width
and returns the number of different paths the insect can take from the
start to the goal. (There is a closed-form solution to this problem,
but try to answer it procedurally using recursion.)
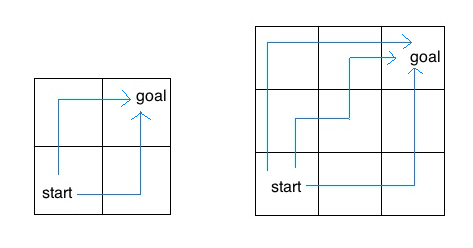
For example, the 2 by 2 grid has a total of two ways for the insect to move from the start to the goal. For the 3 by 3 grid, the insect has 6 diferent paths (only 3 are shown above).
def paths(m, n):
"""Return the number of paths from one corner of an
M by N grid to the opposite corner.
>>> paths(2, 2)
2
>>> paths(5, 7)
210
>>> paths(117, 1)
1
>>> paths(1, 157)
1
"""
"*** YOUR CODE HERE ***"
if m == 1 or n == 1:
return 1
return paths(m - 1, n) + paths(m, n - 1)Use OK to test your code:
python3 ok -q pathsQuestion 3: G function
A mathematical function G on positive integers is defined by two
cases:
G(n) = n, if n <= 3
G(n) = G(n - 1) + 2 * G(n - 2) + 3 * G(n - 3), if n > 3Write a recursive function g that computes G(n).
def g(n):
"""Return the value of G(n), computed recursively.
>>> g(1)
1
>>> g(2)
2
>>> g(3)
3
>>> g(4)
10
>>> g(5)
22
"""
"*** YOUR CODE HERE ***"
if n in (1, 2, 3):
return n
return g(n-1) + 2*g(n-2) + 3*g(n-3)
# Iterative solution, if you're curious
def g_iter(n):
"""Return the value of G(n), computed iteratively.
>>> g_iter(1)
1
>>> g_iter(2)
2
>>> g_iter(3)
3
>>> g_iter(4)
10
>>> g_iter(5)
22
"""
if n == 1 or n == 2 or n == 3:
return n
a, b, c = 1, 2, 3
while n > 3:
a, b, c = b, c, c + 2*b + 3*a
n = n - 1
return cUse OK to test your code:
python3 ok -q gSubmit
Make sure to submit this assignment by running:
python3 ok --submit