Lab 2: Environments and Higher Order Functions
Due at 11:59:59 pm on 09/15/2020.
Starter Files
Download lab02.zip. Inside the archive, you will find starter files for the questions in this lab, along with a copy of the OK autograder.
Submission
By the end of this lab, you should have submitted the lab with python3 ok --submit. You may submit more than once before the deadline; only the final submission will be graded. Check that you have successfully submitted your code on okpy.org. See this article for more instructions on okpy and submitting assignments.
- To receive full credit for this lab, all questions 1 - 5 must be attempted. Question 6 are optional.
When you are ready to submit, run ok with the --submit option:
python3 ok --submitAfter submitting, ok will display a submission URL, with which you can view your submission on okpy.org.
Introduction
In the last lab, you learned some basic expressions and wrote some python code. In this lab, we will introduce you to environments and explore higher order functions (HOFs).
Python Tutor
Python tutor is a website that allows you to write python code in your web browser and see it visualized step by step. Before we explain more, let’s experiment with it a little. First, head to the python tutor website
Copy and paste this code snippet into the box:
y = 3
x = 5
z = y + x
print(z)Press “visualize execution”
You can press the “forward” and “back” buttons to step forward or backwards in the code. Every time you step forward, python will run that line of code. Notice the legend on the bottom left of the visualizer that tells you what the color of the arrows mean.
You may notice that when you press the forward button for the first time, something pops up on the right side of the screen.

Given the line that you just ran, what do you think this diagram means? Try running a few more lines.
What python tutor is doing is showing you exactly what each variable is and what its value is., It shows you the output of the print statement in the box above the diagram.

What’s the difference between the value that appears in the interpreter after evaluating an expression and the output displayed by a print statement?
The value that appears after evaluating is a feature that only the interpreter has. When you actually run the code from a file, that return value does not get printed. The print statement actually does print directly to your terminal.
Python tutor is a great tool because it helps you understand exactly what your code is doing and also keeps track of what variables’ values are along the way. If you ever have trouble understanding what your code is doing, or finding a bug, pull up python tutor and step through it!
When we assign variables, python tutor visualizes this with the variable’s name and a box next to it with the variable’s value. This is just what a variable is! Something that can get assigned a value.
The frame is called “global” for a reason. We will explain that later on.
Let’s throw a function in there. Copy and paste this into the python tutor:
from operator import add
y = 3
x = 5
z = add(x,y)
print(z)If you step until step 5, we see that there is something under the “objects” category.
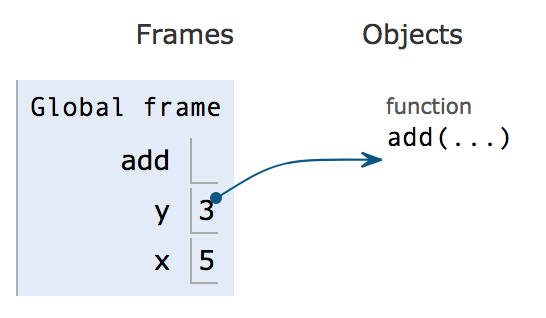
Add is a function, and functions live in object land. We denote which names correspond to which functions with an arrow.
You can think of everything in “frame land” as a box. The box holds something, but is not the thing itself. Some boxes hold integers directly, like the values of x and y in the above image. Other boxes hold more complicated things like functions which cannot be stored directly in the box. Instead, the box holds a pointer to the function which actually lives in object land. In this lab, we are not worried about that, we want you to pay attention to the boxes.
What about floats, booleans, and strings? They also live inside the box, as seen below.

Now that you understand a little bit of how python tutor works, let’s write a function to visualize.
Functions and Python Tutor
Let’s see what function calls look like in the python interpreter.
Paste this code into the interpreter. If you are not in edit mode, click the “edit this code” hyperlink.
def sum(x,y):
z = x + y
return z
x = 3
y = 4
z = sum(x,y)
a = z + 1Now step through the code. Notice in step 5 something interesting happens. A new frame pops up and the execution arrow miraculously moves all the way to the first line. How did we get back there? Think about what would cause this jump before reading the answer below.
When we call the sum function, we need to step through the function itself and execute all of its lines. Where is the function defined? In line 1! Thus, the python interpreter needs to go back there and step through each individual line.
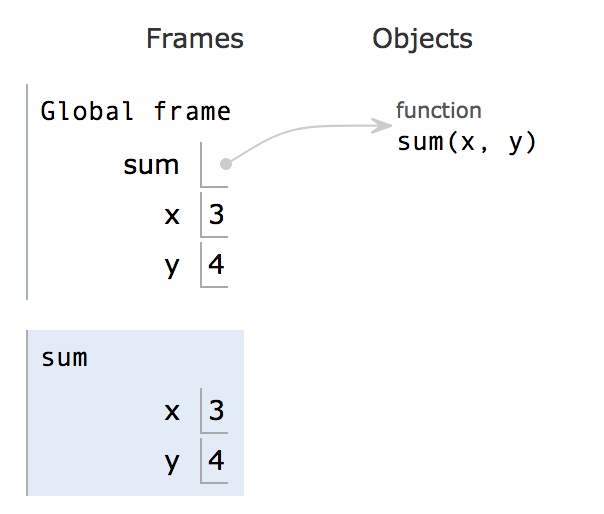
This new frame seen above is a local frame. It is a frame for the sum function that was just called. Everything that happens inside the sum function will be shown inside sum’s local frame.
Step through the rest of the code to see what happens.
Notice that between steps 8 and 9, the function jumps from line 3 to line 6. What’s that all about? Why doesn’t it just go straight to line 4?
Remember how the interpreter had to jump into the sum function to execute it? Well, when it finishes the function, it needs to jump back to the line it was running before the function. That line was line 6.
Now, let’s see what happens if a function calls a function. Copy the following code into python tutor.
def sum(x,y):
z = x + y
return z
def square_sum(x,y):
z = 2
return sum(x, y)**z
x = 3
y = 4
square_sum(x,y)Now press “forward” 2 times.
You may notice that during steps 1 and 2, the visualizer skips over the bodies of the functions. This is because the functions have not been called yet, so the python interpreter will not unpack the function and go into it. It only notes that there are two functions named sum and square_sum, and assigns them to functions living in object land.
Try clicking forward to step 6. In step 6, the interpreter enters the square_sum function. See the new local frame that appeared.
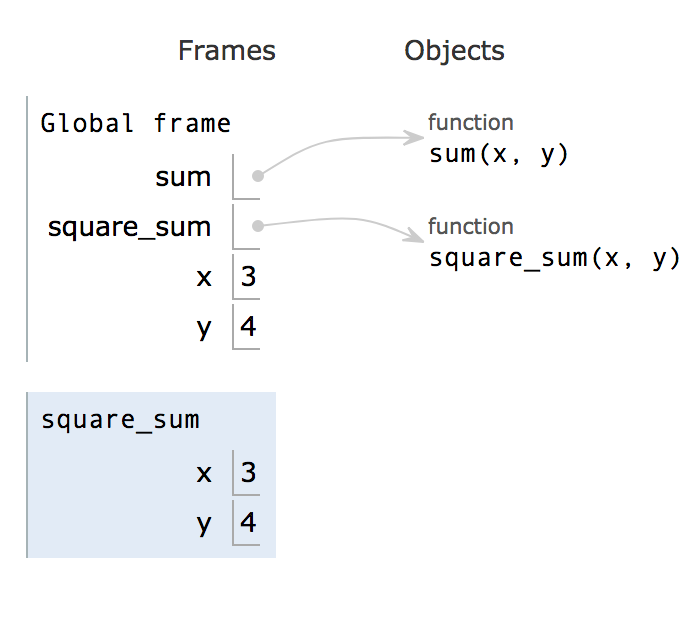
Fun fact: Because the frames are stacked this way, we call the group of frames the call stack.
If you click forward one more time, you’ll see z pop up, which is set to 2. Then, we enter the sum function. Step to step 11.
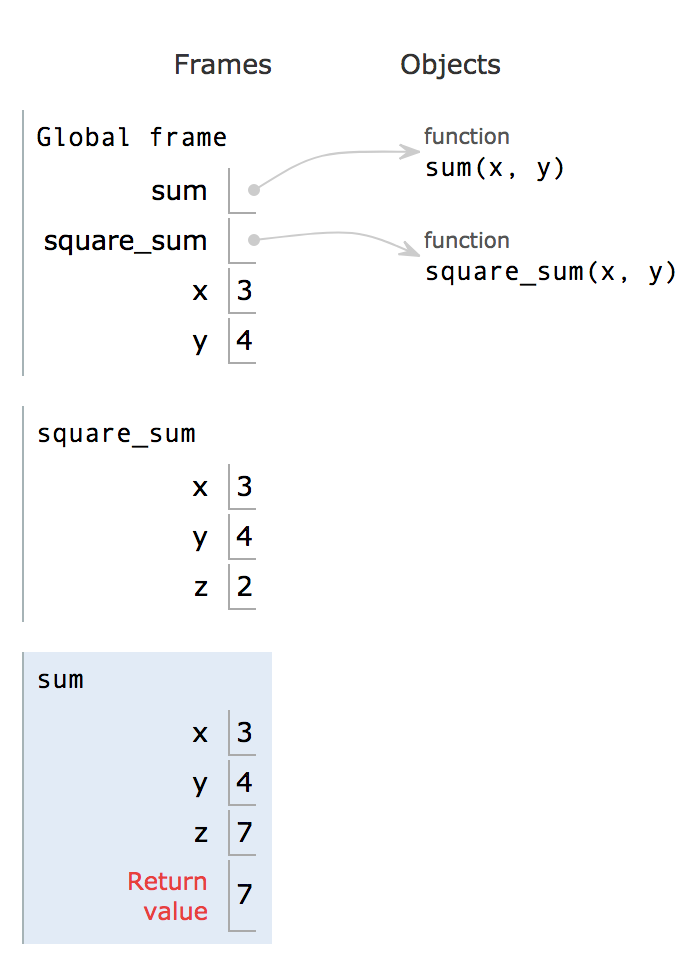
At this point, you see that we have many variables all names the same thing. How does python know which variable we are referring to when we want the value of “x”? Is it the first, the second, or the third?
This is where scope comes in.
Everything inside a function’s local frame is said to be in its “scope”. A functions scope contains all the variables and functions it can access/manipulate/use.
There are two big categories for scope: local and global.
- Global scope is just whatever lies in the global frame.
- Local scope is the scope of any individual function.
When we are in the sum function, when we ask for z, we will retrieve z in sum’s local frame. When we are in square_sum, we will retrieve the z in square_sum’s local frame.
Let’s continue exploring our function.
After returning from sum, we go back to the line where we called sum: 6. Now that we have the result of sum (7), we can raise it to the power of z, which is 2, and return it.
Now that you’ve seen a bit of defining functions, calling functions, and how both look like when they are visualized in python tutor, we will move on to learning about text editors.
Scopes and Nested Functions
Let’s see what nested function calls look like in the python interpreter.
Paste this code into the interpreter or follow this link Ex1
def bonus(score):
previousScore = score
multiplier = 1
if score > 25:
multiplier = 2
score *= multiplier
return score
print(bonus(score))
print(previousScore)Now step through the code. Why does it error out? The error message reads
NameError: name 'previousScore' is not definedBut didn't we define previousScore in the body of the bonus function? We did, but that previousScore is only defined in the scope of the function. So it is not accessible outside in the global scope.
Let's try another function Ex2
def totalScore(score):
multiplier = 2
def bonus(score):
if score > 25:
score *= multiplier
else:
score /= multiplier
return score
return score, bonus(score)
score = 12
totalScore(score)
print(score)There's a lot to unpack here. We purposefully gave the variables the same names so you can see how python lookups values for variables. The general principle is that python looks for the value in the current scope first. If it can't find the variable there, it checks it's parent scope, and the parent's parent, all the way up to the global scope. If the variable still isn't found there, an error is raised. Walk through the lookup for multiplier on line 7 in your head as a sanity check.
Functions as Arguments (Funargs)
So far we have used several types of data - ints, floats, booleans, strings, lists, tuples, and numpy.arrays. We perform operations on them by constructing expressions; we assign them to variables; we pass them to functions and return them as results. So what about functions themselves? So far we have called them, that is we applied them to arguments. Sometimes we compose them - just like in math; apply a function to the result of applying a function. You did that several times above.
In modern programming languages like Python, functions are first class citizens;
we can pass them around and put them in data structures. Take a look at the following
and try it out for various functions that you have available in the .py file for this
lab.
>>> square(square(3))
81
>>> square
<function square at 0x102033d90>
>>> x = square
>>> x(3)
9
>>> x(x(2))
16
>>>Higher Order Functions
Thus far, in Python Tutor, we’ve visualized Python programs in the form of environment diagrams that display which variables are tied to which values within different frames. However, as we noted when introducing Python, values are not necessarily just primitive expressions or types like float, string, integer, and boolean.
In a nutshell, a higher order function is any function that takes a function as a parameter or provides a function has a return value. We will be exploring many applications of higher order functions.
Let's think about a more practical use of higher order functions. Pretend you’re a math teacher, and you want to teach your students how coefficients affect the shape of a parabola.
Open Python Tutor in a new tab
Paste this code into the interpreter:
def define_parabola(a, b, c):
def parabola(x):
return a*(x**2) + b*x + c
return parabola
parabola = define_parabola(-2, 3, -4)
y1 = parabola(1)
y2 = parabola(10)
print(y1, y2)Now step through the code. In the define_parabola function, the coefficient values of 'a', 'b', and 'c' are taken in, and in return, a parabolic function with those coefficient values is returned.
As you step through the second half of the code, notice how the value of parabola points at a function object! The define_parabola higher order nature comes from the fact that its return value is a function.
Another thing noting is where the pointer moves after the parabola function is called. Notice that the pointer goes to line 2, where parabola was originally defined. In a nutshell, this example is meant to show how a closure is returned from the define_parabola function.
Question 1: Applying Function Arguments
def square(x):
return x * x
def twice(f,x):
"""Apply f to the result of applying f to x"
>>> twice(square,3)
81
"""
"*** YOUR CODE HERE ***"
return f(f(x))Use OK to test your code:
python3 ok -q twicedef increment(x):
return x + 1
def apply_n(f, x, n):
"""Apply function f to x n times.
>>> apply_n(increment, 2, 10)
12
"""
"*** YOUR CODE HERE ***"
res = x
for i in range(n):
res = f(res)
return resUse OK to test your code:
python3 ok -q apply_nQuestion 2: Flight of the Bumblebee
Write a function that takes in a number n and returns a function
that takes in a number m which will print all numbers from 0
to m - 1 (including 0 but excluding m) but print Buzz!
instead for all the numbers that are divisible by n.
def make_buzzer(n):
""" Returns a function that prints numbers in a specified
range except those divisible by n.
>>> i_hate_fives = make_buzzer(5)
>>> i_hate_fives(10)
Buzz!
1
2
3
4
Buzz!
6
7
8
9
"""
"*** YOUR CODE HERE ***"
def buzz(m):
i = 0
while i < m:
if i % n == 0:
print('Buzz!')
else:
print(i)
i += 1
return buzzUse OK to test your code:
python3 ok -q make_buzzerQuestion 3: Piecewise
Implement piecewise, which takes two one-argument functions, f and g,
along with a number b. It returns a new function that takes a number x and
returns either f(x) if x is less than b, or g(x) if x is greater than
or equal to b.
def piecewise(f, g, b):
"""Returns the piecewise function h where:
h(x) = f(x) if x < b,
g(x) otherwise
>>> def negate(x):
... return -x
>>> def identity(x):
... return x
>>> abs_value = piecewise(negate, identity, 0)
>>> abs_value(6)
6
>>> abs_value(-1)
1
"""
"*** YOUR CODE HERE ***"
def h(x):
if x < b:
return f(x)
return g(x)
return hUse OK to test your code:
python3 ok -q piecewiseQuestion 4: Funception
Write a function (funception) that takes in another function func_a and a number start and returns a function (func_b) that will have one parameter to take in the stop value.
func_b should take the following into consideration the following in order:
- Takes in the stop value.
- If the value of
startis less than 0, it should exit the function. - If the value of
startis greater than stop, applyfunc_aonstartand return the result. - If not, apply
func_aon all the numbers from start (inclusive) up to stop (exclusive) and return the product.
def funception(func_a, start):
""" Takes in a function (function A) and a start value.
Returns a function (function B) that will find the product of
function A applied to the range of numbers from
start (inclusive) to stop (exclusive)
>>> def func_a(num):
... return num + 1
>>> func_b1 = funception(func_a, 3)
>>> func_b1(2)
4
>>> func_b2 = funception(func_a, -2)
>>> func_b2(-3)
>>> func_b3 = funception(func_a, -1)
>>> func_b3(4)
>>> func_b4 = funception(func_a, 0)
>>> func_b4(3)
6
>>> func_b5 = funception(func_a, 1)
>>> func_b5(4)
24
"""
"*** YOUR CODE HERE ***"
def func_b(stop):
i = start
product = 1
if start < 0:
return None
if start > stop:
return func_a(start)
while i < stop:
product *= func_a(i)
i += 1
return product
return func_bUse OK to test your code:
python3 ok -q funceptionQuestion 5: I Heard You Liked Functions...
Define a function cycle that takes in three functions f1, f2,
f3, as arguments. cycle will return another function that should
take in an integer argument n and return another function. That
final function should take in an argument x and cycle through
applying f1, f2, and f3 to x, depending on what n
was. Here's the what the final function should do to x for a few
values of n:
n = 0, returnxn = 1, applyf1tox, or returnf1(x)n = 2, applyf1toxand thenf2to the result of that, or returnf2(f1(x))n = 3, applyf1tox,f2to the result of applyingf1, and thenf3to the result of applyingf2, orf3(f2(f1(x)))n = 4, start the cycle again applyingf1, thenf2, thenf3, thenf1again, orf1(f3(f2(f1(x))))- And so forth.
Hint: most of the work goes inside the most nested function.
def cycle(f1, f2, f3):
""" Returns a function that is itself a higher order function
>>> def add1(x):
... return x + 1
>>> def times2(x):
... return x * 2
>>> def add3(x):
... return x + 3
>>> my_cycle = cycle(add1, times2, add3)
>>> identity = my_cycle(0)
>>> identity(5)
5
>>> add_one_then_double = my_cycle(2)
>>> add_one_then_double(1)
4
>>> do_all_functions = my_cycle(3)
>>> do_all_functions(2)
9
>>> do_more_than_a_cycle = my_cycle(4)
>>> do_more_than_a_cycle(2)
10
>>> do_two_cycles = my_cycle(6)
>>> do_two_cycles(1)
19
"""
"*** YOUR CODE HERE ***"
def ret_fn(n):
def ret(x):
i = 0
while i < n:
if i % 3 == 0:
x = f1(x)
elif i % 3 == 1:
x = f2(x)
else:
x = f3(x)
i += 1
return x
return ret
return ret_fnUse OK to test your code:
python3 ok -q cycleSubmit
Make sure to submit this assignment by running:
python3 ok --submitOptional Extra Practice Open in a new window
These questions are a mix of Parsons Problems, Code Tracing questions, and Code Writing questions. For lab 3 and onward, these questions are required, but they are optional for lab 2.
Confused about how to use the tool? Check out https://codestyle.herokuapp.com/cs88-lab01 for some problems designed to demonstrate how to solve these types of problems.
These cover some similar material to lab, so can be helpful to further review or try to learn the material. Unlike lab and homework, after you've worked for long enough and tested your code enough times on any of these questions, you'll have the option to view an instructor solution. You'll unlock each question one at a time, either by correctly answering the previous question or by viewing an instructor solution.
Use OK to test your code:
python3 ok -q extra_practiceMore FUN with FUNctions (Optional)
The question in lab02_extra.py is optional - it's for you to solve if you want more practice with functions. Be warned it's a challenge!
Question 6: Church numerals
The logician Alonzo Church invented a system of representing non-negative integers entirely using functions. The purpose was to show that functions are sufficient to describe all of number theory: if we have functions, we do not need to assume that numbers exist, but instead we can invent them.
Your goal in this problem is to rediscover this representation known as Church
numerals. Here are the definitions of zero, as well as a function that
returns one more than its argument:
def zero(f):
def _zero(x):
return x
return _zero
def successor(n):
def _succ(f):
def t(x):
return f(n(f)(x))
return t
return _succFirst, define functions one and two such that they have the same behavior
as successor(zero) and successsor(successor(zero)) respectively, but do
not call successor in your implementation.
def one(f):
"""Church numeral 1: same as successor(zero)"""
"*** YOUR CODE HERE ***"
def _one(x):
return f(x)
return _one
def two(f):
"""Church numeral 2: same as successor(successor(zero))"""
"*** YOUR CODE HERE ***"
def _two(x):
return f(f(x))
return _twoNext, implement a function church_to_int that converts a church numeral
argument to a regular Python integer.
def church_to_int(n):
"""Convert the Church numeral n to a Python integer.
>>> church_to_int(zero)
0
>>> church_to_int(one)
1
>>> church_to_int(two)
2
>>> church_to_int(three)
3
"""
"*** YOUR CODE HERE ***"
return n(lambda x: x + 1)(0)Use OK to test your code:
python3 ok -q church_to_intFinally, implement functions add_church, mul_church, and pow_church that
perform addition, multiplication, and exponentiation on church numerals.
def add_church(m, n):
"""Return the Church numeral for m + n, for Church numerals m and n.
>>> church_to_int(add_church(two, three))
5
"""
"*** YOUR CODE HERE ***"
return lambda f: lambda x: m(f)(n(f)(x))
def mul_church(m, n):
"""Return the Church numeral for m * n, for Church numerals m and n.
>>> four = successor(three)
>>> church_to_int(mul_church(two, three))
6
>>> church_to_int(mul_church(three, four))
12
"""
"*** YOUR CODE HERE ***"
return lambda f: m(n(f))
def pow_church(m, n):
"""Return the Church numeral m ** n, for Church numerals m and n.
>>> church_to_int(pow_church(two, three))
8
>>> church_to_int(pow_church(three, two))
9
"""
"*** YOUR CODE HERE ***"
return n(m)Use OK to test your code:
python3 ok -q add_church
python3 ok -q mul_church
python3 ok -q pow_churchChurch numerals are a way to represent non-negative integers via
repeated function application. The definitions of zero, one, and
two show that each numeral is a function that takes a function and
repeats it a number of times on some argument x.
The church_to_int function reveals how a Church numeral can be mapped
to our normal notion of non-negative integers using the increment
function.
Addition of Church numerals is function composition of the functions of
x, while multiplication (added to the question for these solutions)
is composition of the functions of f.